独学 で大学数学の 微分方程式 を勉強 したいと思ったことありませんか?
実は、僕も大学数学の 微分方程式 を 独学 で学びたいと思い勉強を始めました。
結果、放送大学の数学のテキスト をほぼ読み終えました。
目次
大学数学の微分方程式
放送大学の数学のテキスト の練習問題の解答は理解できるほどには詳細に書かれていないので自分で出した解答を載せています。
URLが放送大学の数学のテキストの該当ページを指しています。
- トラクトリックス
- 1階非斉次線形微分方程式
- 変数分離形
- 同次形
- 包絡線
- 部分積分
- 定数変化法
- 未定係数法
- 初期値問題
- 階数低下法
- 連立微分方程式
- オイラーの微分方程式
- フロベニウスの方法
- 級数解法
- 境界条件
- 調和多項式
- ラプラシアン
- 積分因子
- 完全微分方程式
トラクトリックス
1/sinxdxから1/tdtへの変形
(1/sinx)dxから(1/t)dtへの変形 に必要な道具
- 倍角の公式
- 半角の公式
\(\frac{1}{sin\ x}dx\)から\(\frac{1}{t}dt\)への変形が複雑だったので記事にしました。

1階非斉次線形微分方程式
1階非斉次線形微分方程式の一般解
1階非斉次線形微分方程式の一般解の導出 を使うと一般解が容易に解けます。

変数分離形
y’=(1+y)/sinxの解き方 変数分離形
y’=(1+y)/sinx の計算過程が複雑なので記事にしました。
計算の方針:1/sinxの積分が複雑なので最初に計算します。
\(y’=\frac{1+y}{sin\ x}\) の計算過程が複雑なので記事にしました。

同次形
y’=(x^2-y^2)/2xyの解き方 同次形
\(y’=\frac{x^2+y^2}{2xy}\)は検索にかかってくるが \(y’=\frac{x^2-y^2}{2xy}\) は検索しても出てこなかったので記事にしました。
同次形 y’=(x^2-y^2)/2xy を解くのに必要な道具:対数関数の置換積分

y’=2y/x-yの解き方 同次形
\(y’=\frac{2y}{x-y}\)の解き方、記事にしました。
y’=2y/x-y を解くのに必要な道具:同次形微分方程式の解法

包絡線
dy/dx-(3/2)(y-a)^(1/3)=0 の一般解と、それらの解曲線の包絡線である特異解
「dy/dx-(3/2)(y-a)^(1/3)=0 の一般解と、それらの解曲線の包絡線である特異解を求めよ」という問題である。
「\(\frac{dy}{dx}-\frac{3}{2}\sqrt[3]{y-a}=0\) の一般解と、それらの解曲線の包絡線である特異解を求めよ」という問題である。
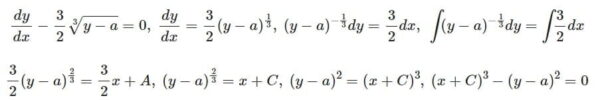
部分積分
x=-e^2t∫3t^2e^(-2t)dt+te^2t∫3te^(-2t)dtの解き方 部分積分
非斉次方程式の特殊解の計算が面倒だったので記事にしました。
x=-e^(2t)∫3t^2e^(-2t)dt+te^(2t)∫3te^(-2t)dt を解くのに必要な道具:部分積分

定数変化法
特殊解を求めるのに 定数変化法 より クラメルの公式
定数係数非斉次線形方程式
$$x”+px’+qx=r(t)$$
の特殊解は
$$x(t)=-x_1(t)\int_{}{}\frac{x_2(t)r(t)}{W(x_1,\ x_2)(t)}dt+x_2(t)\int_{}{}\frac{x_1(t)r(t)}{W(x_1,\ x_2)(t)}dt$$
である。
定数係数非斉次2階線形方程式の特殊解を求めるのに 定数変化法 があるが クラメルの公式 が使われている方が式を覚えるのが楽でした。

未定係数法
x”-x’=sint+2costの一般解(未定係数法)
x”-x’=sint+2cost の一般解を未定係数法で解いたら計算が楽でした。
x”-x’=sint+2cost を解くのに必要な道具:未定係数法
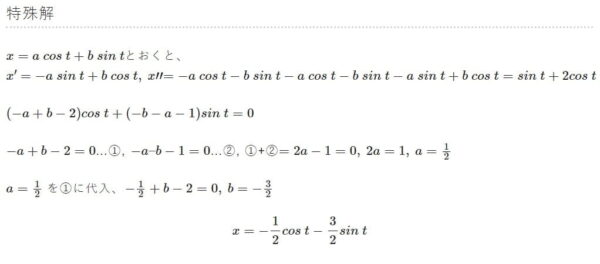
初期値問題
x”-2x’+5x=20cost, x(0)=x'(0)=0の解き方 初期値問題
初期値問題 x”-2x’+5x=20cost, x(0)=x'(0)=0 の計算が長くなったので記事にしました。
x”-2x’+5x=20cost, x(0)=x'(0)=0 を解くのに必要な道具:特性方程式が虚数解の場合の一般解

階数低下法
(t+2)x”-(2t+6)x’+(t+4)x=0 (x=e^t)の一般解 階数低下法
階数低下法 (t-2)x”-(2t-6)x’+(t-4)x=0 (x=e^t)も同じ手順で解法出来ます。
(t+2)x”-(2t+6)x’+(t+4)x=0 (x=e^t) を解くのに必要な道具:階数低下法

(t^2+3t+4)x”+(t^2+t+1)x’-(2t+3)x=0 (x=e^(-t))の一般解 階数低下法
\((t^2+3t+4)x”+(t^2+t+1)x’-(2t+3)x=0\ (x=e^{-t})\) の解くのに苦労したので備忘録として記事にしました。
(t^2+3t+4)x”+(t^2+t+1)x’-(2t+3)x=0 (x=e^(-t))の解くのに必要な道具:階数低下法
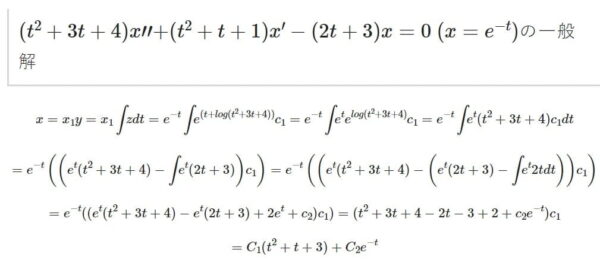
連立微分方程式
3つの関数の積の積分
3つの関数の積の積分 が3つの関数の積の導関数の公式の逆演算で解けるのではないかと思い試してみました。

オイラーの微分方程式
4xy”+2y’+y=0の解き方(オイラーの微分方程式)
4xy”+2y’+y=0 はオイラーの微分方程式の変数変換を使うと解けたので記事にしました。
4xy”+2y’+y=0 を解くのに必要な道具
オイラーの微分方程式:\( t^2\frac{d^2x}{dt^2}+pt\frac{dx}{dt}+qx=0\)

フロベニウスの方法
4xy”+2y’+y=0の解き方(フロベニウスの方法)
4xy”+2y’+y=0 を フロベニウスの方法 で解くのに苦労したので記事にしました。
4xy”+2y’+y=0 を解くのに必要な道具
- フロベニウスの方法
- 三角関数のマクローリン展開

x^2y”-2xy’+(x^2+2)y=0の解き方(フロベニウスの方法)
\(x^2y”-2xy’+(x^2+2)y=0\)を フロベニウスの方法 で解くのに苦労したので記事にしました。
x^2y”-2xy’+(x^2+2)y=0 を解くのに必要な道具
- フロベニウスの方法
- 三角関数のマクローリン展開

級数解法
級数解法・フロベニウスの方法 使い分け
線形微分方程式の 級数解法 とフロベニウスの方法、どちらを使うべきか混乱していたので整理しておきます。

境界条件
x=0 で 等温境界条件 u(0,t)=uをみたし、 x=1 で 断熱境界条件 ux(1,t)=0をみたす解
x=0 で 等温境界条件 u(0,t)=uをみたし、 x=1 で 断熱境界条件 ux(1,t)=0をみたす解 を求めるのに必要な道具
- 熱伝導を表す偏微分方程式
- 重ね合わせの原理

x=0 で 断熱境界条件 ux(0,t)=uをみたし、 x=1 で 等温境界条件 u(1,t)=0 をみたす解
x=0 で 断熱境界条件 ux(0,t)=uをみたし、 x=1 で 等温境界条件 u(1,t)=0 をみたす解 を求めるのに必要な道具
- 熱伝導を表す偏微分方程式
- 重ね合わせの原理
\(x=0\)で断熱境界条件\(u_x(0,t)=0\)をみたし、\(x=1\)で等温境界条件\(u(1,t)=0\)をみたす解

調和多項式
4x^7y-28x^5y^3+28x^3y^5-4xy^7をr^nsinnθ,r^ncosnθの1次結合として表す。
4x^7y-28x^5y^3+28x^3y^5-4xy^7 を r^nsinnθ,r^ncosnθ の1次結合 として表す問題
\(4x^7y-28x^5y^3+28x^3y^5-4xy^7\)が調和多項式であることを確かめ、それを極座標に変換して、\(r^n sin\ n \theta, r^n cos\ n \theta\)の1次結合として表す問題。

ラプラシアン
4x^7y-28x^5y^3+28x^3y^5-4xy^7の最大値・最小値
4x^7y-28x^5y^3+28x^3y^5-4xy^7 を単位円の境界である単位円周x^2+y^2=1で考えたとき、最大値と最小値 を求める問題
\(4x^7y-28x^5y^3+28x^3y^5-4xy^7\)を単位円の境界である単位円周\(x^2+y^2=1\)で考えたとき、最大値と最小値を求める問題

積分因子
独学で大学数学の積分因子を勉強しています!

完全微分方程式
完全微分形の一般解
完全微分形の一般解を導出する方法で一般解を求める。

(x^2+3xy+2y^2)dy+(2x^2+3xy+y^2)dx=0の一般解
\((x^2+3xy+2y^2)dy+(2x^2+3xy+y^2)dx=0\)を完全微分形の一般解を導出する方法で求める。

検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
![]() を利用してみてはいかがでしょうか。
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
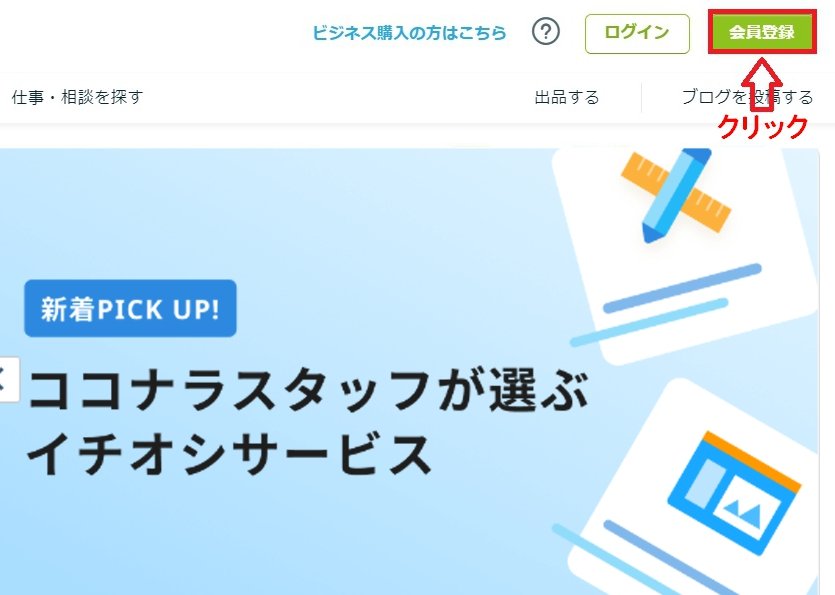
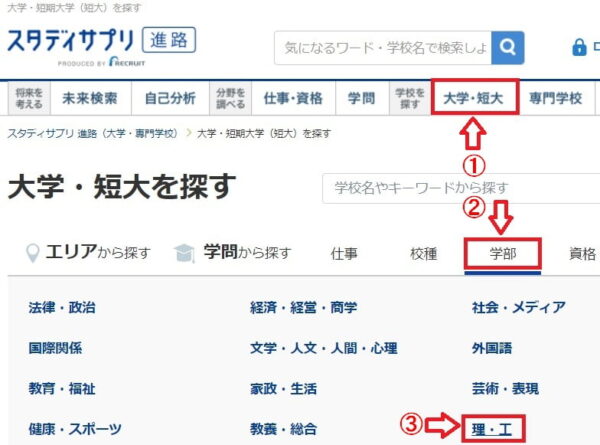
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
独学で大学数学を勉強する順番
- 独学で大学数学入門(高校数学の復習)
- 独学で大学数学の微分積分を勉強しています!
- 独学で大学数学の解析入門を勉強しています!
- 独学で大学数学の微分方程式を勉強しています!
- MathJax とは
- スタディサプリ進路 社会人向け の 使い方