定数係数非斉次2階線形方程式の 特殊解 を求めるのに 定数変化法 があるが クラメルの公式 が使われている方が式を覚えるのが楽でした。
目次
定数変化法
定数係数非斉次線形方程式
$$x”+px’+qx=r(t)$$
の特殊解は
$$x(t)=-x_1(t)\int_{}{}\frac{x_2(t)r(t)}{W(x_1,\ x_2)(t)}dt+x_2(t)\int_{}{}\frac{x_1(t)r(t)}{W(x_1,\ x_2)(t)}dt$$
である。
クラメルの公式
連立方程式
$$\left\{ \begin{array}{r} a_{11}x_1+a_{12}x_2=b_1 \\ a_{21}x_1+a_{22}x_2=b_2 \end{array} \right.$$
を行列を用いて表すと
$$\left( \begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right)\left( \begin{array}{c} x_1 \\ x_2 \end{array} \right)=\left( \begin{array}{c} b_1 \\ b_2 \end{array} \right)$$
の解は
$$x_1=\frac{\left| \begin{array}{cc} b_1 & a_{12} \\ b_2 & a_{22} \end{array} \right|}{\left|\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right|},\ x_2=\frac{\left| \begin{array}{cc} a_{11} & b_1 \\ a_{21} & b_2\end{array} \right|}{\left|\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right|}$$
特殊解 を求めるのに 定数変化法 より クラメルの公式
x”-x’=sint+2costの一般解(定数変化法)
\(x”-x’=sin\ t+2cos\ t\)の一般解の計算が複雑なので記事にしました。
x”-x’=sint+2cost を解くのに必要な道具
- 部分積分
- 定数変化法

x”-x’-6x=5tの一般解(定数変化法)
x”-x’-6x=5tの特殊解 を求めるのに必要な道具
- 定数変化法
- クラメルの公式 定数変化法
定数係数非斉次2階線形方程式の特殊解を求めるのに定数変化法があるが クラメルの公式 が使われてい方が式を覚えるのが楽でした。

x”-x’=sint+2costの一般解(クラメルの公式)
x”-x’=sint+2cost を解くのに必要な道具
- 部分積分
- 定数変化法クラメルの公式
定数係数非斉次2階線形方程式の特殊解を求めるのに定数変化法があるが クラメルの公式 が使われている方が式を覚えるのが楽でした。

検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
![]() を利用してみてはいかがでしょうか。
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
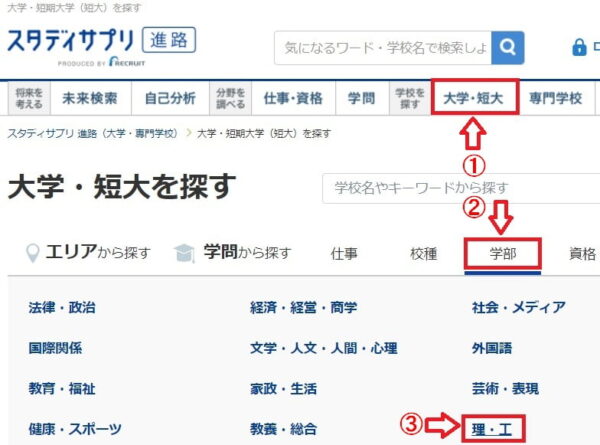
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
独学で大学数学の微分方程式を勉強しています!
- 独学で大学数学入門(高校数学の復習)
- 独学で大学数学の微分積分を勉強しています!
- 独学で大学数学の解析入門を勉強しています!
- 独学で大学数学の微分方程式を勉強しています!
- MathJax とは
- スタディサプリ進路 社会人向け の 使い方
