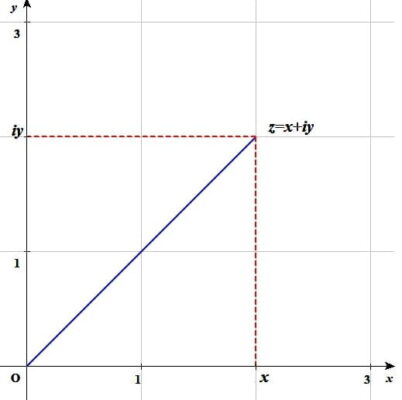
複素数z=x+yiに対して座標平面上の点(x,y)を対応させることによって、座標平面を複素数の全体であると考えることができます。このときの座標平面を 複素数平面 といいます。
複素数平面 ではx軸を実軸、y軸を虚軸といいます。
目次
複素数平面 上の2つの円の交点を求め方
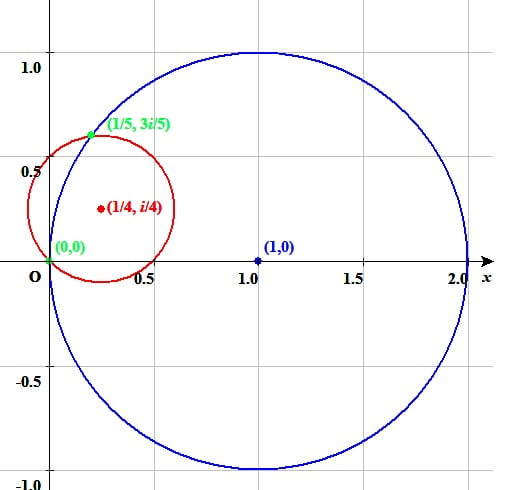
複素数平面上の2つの円\(|w-1|=1と\left|w-\frac{1+i}{4}\right|=\frac{\sqrt{2}}{4}\)の交点の求め方
複素数平面上の 2つの円 |w-1|=1 と |w-(1+i)/4|=√2/4 の交点を求めるのに必要な道具
- 共役複素数の性質
- 複素数の絶対値の性質
複素数平面上の 2つの円 |w-1|=1 と |w-(1+i)/4|=√2/4 の交点を求めるのに必要な道具 共役複素数の性質 複素数の絶対値の性質 複素数平面…
jikuu.work
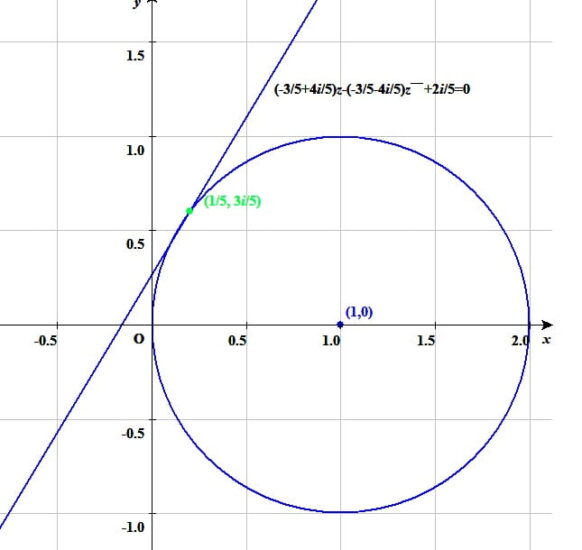
複素数平面 上における中心(1, 0)半径1の円周上の点(1/5, (3i/5)における円の接線の方程式
複素数平面上における中心(1, 0)半径1の円周上の点\(\left(\frac{1}{5},\ \frac{3}{5}i\right)\) における円の接線の方程式
複素数平面上 における円の 接線の方程式 を求めるの必要な道具
- 複素数平面上における円の接線の方程式
- 複素数平面の直線の方程式の一般形
複素数平面上 における中心(1, 0)半径1の円周上の点\(\left(\frac{1}{5},\ \frac{3}{5}i\right)\) における円の 接…
jikuu.work
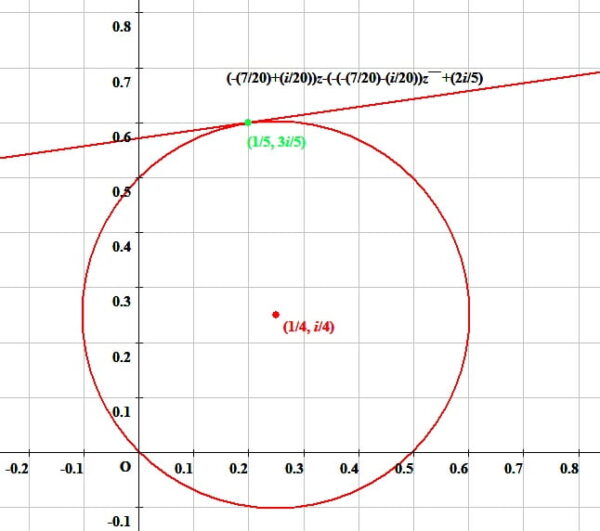
複素数平面上における中心(1/4, i/4)半径1/(2√2)の円周上の点(1/5, (3i/5)における円の接線の方程式
複素数平面上における中心\(\left(\frac{1}{4},\ \frac{1}{4}i\right)\)半径\(\frac{1}{2\sqrt{2}}\)の円周上の点\(\left(\frac{1}{5},\ \frac{3}{5}i\right)\) における円の接線の方程式
複素数平面上 における円の 接線の方程式 を求めるの必要な道具
- 複素数平面上における円の接線の方程式
- 複素数平面の直線の方程式の一般形
複素数平面上 における中心\(\left(\frac{1}{4},\ \frac{1}{4}i\right)\)半径\(\frac{1}{2\sqrt{2}}\…
jikuu.work
検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
![]() を利用してみてはいかがでしょうか。
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
ココナラ 登録方法 会員登録しなくてもサービスの検索はできます。サービスの購入・出品には会員登録が必要です。会員登録をクリック メールアドレスを入力して メール…
jikuu.site
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
スタディサプリ進路 社会人向け の 使い方 スタディサプリ進路 社会人向け の 使い方 スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます…
jikuu.work
独学で大学数学の解析入門を勉強しています!
- ∫∫Kdxdy K:x^2+y^2<=1, y>=0の解き方 累次積分
- 独学で大学数学の重積分に勉強をしています!
- ∫∫D√(x^2 + y^2)dxdy D:x>= 0, y>=0, x^2+y^2<=1, x^2+y^2>=xの解き方 極座標変換
- ∫∫∫Vdxdydz V:x>=0, y>=0, z>=0, √x+√y+√z<=1の解き方 空間極座標
- lim[z→1+i](z^2-iz-1-i)/(z^2-2i)の解き方 複素関数
- ∫(C)Imzdz C:|z-1|=1の解き方 複素積分
- ∫C(z-3)/(z^2-2z+5)dz C:|z-1+i|=2の解き方 コーシーの積分公式
- ∫C(z-3)/(z^2-2z+5)dz C:|z-1-i|=2の解き方 コーシーの積分公式
- 独学で大学数学の留数を勉強しています!
- f”(z)+f(z)=0の解き方 微分方程式
- e^(-x^2-y^2)(ax^2+by^2)の極値
- z=(x+y)/(x^2+y^2+1)の最大値・最小値
- 表面積が一定な直方体のうち体積が最大になるもの
- 独学で大学数学の 複素数平面 上の図形を勉強しています!
独学 で大学数学の 解析入門 を勉強 したいと思ったことありませんか? 実は、僕も大学数学の 解析入門 を 独学 で学びたいと思い勉強を始めました。 結果、放送…
jikuu.work