∫∫Kdxdy K:x^2+y^2=0 の解き方累次積分

∫∫Kdxdy K:x^2+y^2<=1 , y>=0 を解くのに必要な道具

累次積分
置換積分
2倍角の公式

$\iint_Kdxdy\ K:x^2+y^2\le1,y\ge0$の解き方を検索しても出てこなかったので記事にしました。

※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。

$\iint_Kdxdy\ K:x^2+y^2\le1,y\ge0$を解くのに必要な道具 ∫∫Kdxdy K:x^2+y^2<=1 , y>=0 を解くのに必要な道具
累次積分
- 重積分とは
- 累次積分
置換積分
conの2倍角の公式
- 証明
$\iint_Kdxdy\ K:x^2+y^2\le1,y\ge0$の解法 ∫∫Kdxdy K:x^2+y^2<=1 , y>=0 の解法
- 置換積分
まとめ
参考文献
独学で大学数学の解析入門を勉強しています！

$\iint_Kdxdy\ K:x^2+y^2\le1,y\ge0$を解くのに必要な道具 ∫∫Kdxdy K:x^2+y^2<=1 , y>=0 を解くのに必要な道具

累次積分
置換積分
2倍角の公式

累次積分

重積分とは

多変数の範囲にわたる積分

Rにおける2重積分(2変数に関する重積分)は $\iint_Rf(x,y)dxdy$ と記されます。

累次積分

(1) $K=\{(x,y)\in R^2\ |\ \varphi_1(x)\le y\le\varphi_2(x),\ a\le x\le b\}$

上の連続関数f(x,y)に対して

$$\iint_Kf(x,y)dxdy=\int_a^b \left(\int_{\varphi_1(x)}^{\varphi_2(x)} f(x,y)dy\right)dx$$

(2) $K=\{(x,y)\in R^2\ |\ \psi_1(y)\le x\le\psi_2(y),\ c\le y\le d\}$

上の連続関数f(x,y)に対して

$$\iint_Kf(x,y)dxdy=\int_a^b \left(\int_{\psi_1(y)}^{\psi_2(y)} f(x,y)dx\right)dy$$

重積分が 1変数関数の積分を2度行う ことによって求められることを意味しています。

1変数関数の積分を2度行うことを 累次積分 といいます。

置換積分

関数f(x)が連続であり、関数φ(t)は微分可能で導関数φ'(t)が連続とする。a=φ(α),b=φ(β)であれば

$$\int_{a}^{b}f(x)dx=\int_{\alpha}^{ \beta }f(\varphi(t))\varphi'(t)dt$$

が成り立ちます。

conの2倍角の公式

$$cos2\theta=2cos^2\theta-1$$

証明

cosの加法定理：cos(α+β)=cosαcosβ−sinαsinβにおいてα=β=θとおくと，
$$cos2\theta=cos\theta cos\theta−sin\theta sin\theta=cos^2\theta−sin^2\theta$$

さらにこの式において，$sin^2\theta+cos^2\theta=1 $を使って$ sin^2\theta $を消すと

$$cos2\theta=2cos^2\theta-1$$

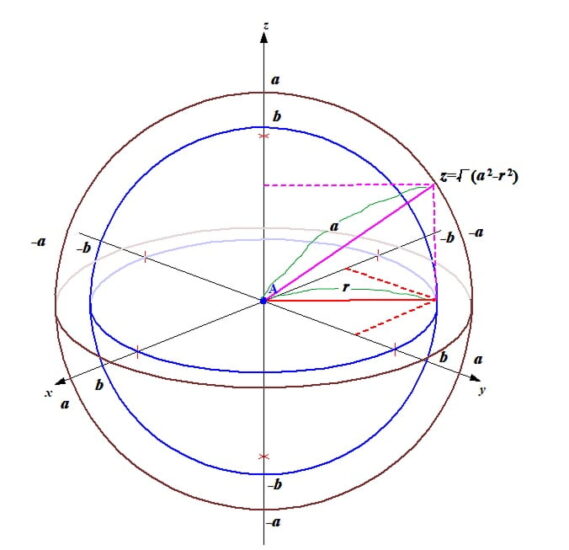
$\iint_Kdxdy\ K:x^2+y^2\le1,y\ge0$の解法 ∫∫Kdxdy K:x^2+y^2<=1 , y>=0 の解法

$$\iint_Kdxdy=\int_{0}^{1}dy\int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}dx=\int_{0}^{1}[x]^{\sqrt{1-y^2}}_{-\sqrt{1-y^2}} dy=\int_{0}^{1}2 \sqrt{1-y^2} dy$$

置換積分

$ 2\sqrt{1-y^2} =t$とおく

$$t^2=4 (1-y^2),\ \frac{t^2}{4}=1-y^2,\ y= \sqrt{1- \frac{t^2}{4} }(=\varphi(t)),\ \frac{dy}{dt}= \frac{1}{2} (1- \frac{1}{4}t^2 )^{- \frac{1}{2} }(- \frac{1}{2}t)=- \frac{1}{4} t(1- \frac{1}{4} t^2)^{- \frac{1}{2} }$$

y=sint(=φ(t))とおく

$$ \frac{dy}{dt} = \varphi'(t) =cos\ t$$

y=0のとき $t=sin^{-1}0=0$ 、y=1のとき $t=sin^{-1}1= \frac{\pi}{2} $

$$\int_{0}^{1}2 \sqrt{1-y^2} dy=\int_{0}^{ \frac{\pi}{2} }2 \sqrt{1-sin^2t}\cdot cos\ tdt=\int_{0}^{ \frac{\pi}{2} } 2cos^2tdt=\int_{0}^{ \frac{\pi}{2} } (1+cos2t)dt$$

$$=\left[t+\frac{sin2t}{2}\right]^{ \frac{\pi}{2}}_{0}= \frac{\pi}{2}$$