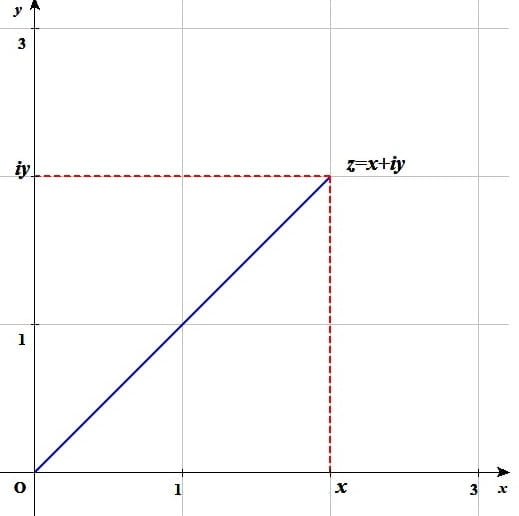
複素数平面上の 2つの円 |w-1|=1 と |w-(1+i)/4|=√2/4 の交点を求めるのに必要な道具
複素数平面上 の2つの円\(|w-1|=1\)と\(\left|w-\frac{1+i}{4}\right|=\frac{\sqrt{2}}{4}\)の交点の求め方
※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。
目次
複素数平面上 の2つの円の交点を求めるのに必要な道具
共役複素数の性質
$$\overline{\alpha-\beta}=\overline{\alpha}-\overline{\beta}$$
複素数の絶対値の性質
$$|z|^2=z\cdot \overline{z}$$
複素数平面上 の2つの円\(|w-1|=1\)と\(\left|w-\frac{1+i}{4}\right|=\frac{\sqrt{2}}{4}\)の交点の求め方 複素数平面上 の 2つの円|w-1|=1と|w-(1+i)/4|=√2/4の交点の求め方
2乗して連立方程式を解く
$$\left\{ \begin{array}{l} (w-1)(\overline{w}-1)=1 \\ (w-\frac{1+i}{4})(\overline{w}-\frac{1-i}{4})=\frac{2}{16} \end{array} \right.$$
\((w-1)(\overline{w}-1)=1\)
$$w\overline{w}-w-\overline{w}=0\cdots①$$
\((w-\frac{1+i}{4})(\overline{w}-\frac{1-i}{4})=\frac{2}{16}\)
$$w\overline{w}-\frac{1-i}{4}w-\frac{1+i}{4}\overline{w}=0\cdots②$$
①-②
$$\frac{-3-i}{4}w+\frac{-3+i}{4}\overline{w}=0,\ \frac{-3+i}{4}\overline{w}=-\frac{-3-i}{4}w,\ \overline{w}=-\frac{-3-i}{-3+i}w$$
$$\overline{w}=-\frac{9-1+6i}{10}w=\frac{-4-3i}{5}w$$
①へ代入
$$\frac{-4-3i}{5}w^2-w-\frac{-4-3i}{5}w=0,\ w^2-\frac{5}{-4-3i}w-w=0,\ w^2-\frac{-20+15i}{25}w-\frac{25}{25}w=0$$
$$\ w^2-\frac{5+15i}{25}w=0,\ w^2-\frac{1+3i}{5}w=0,\ w\left(w-\frac{1+3i}{5}\right)=0$$
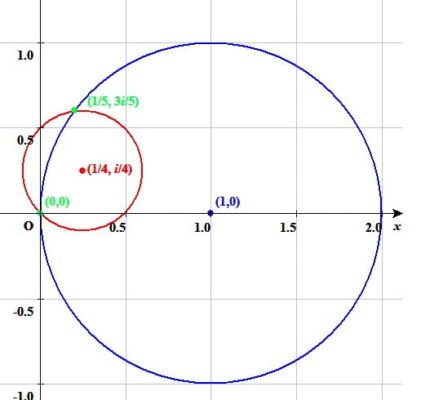
|w-1|=1と\(\left|w-\frac{1+i}{4}\right|=\frac{\sqrt{2}}{4}\)の交点は |w-1|=1と|w-(1+i)/4|=√2/4の交点
$$(0,\ 0),\ \left(\frac{1}{5},\ \frac{3i}{5}\right)$$
参考文献
検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
![]() を利用してみてはいかがでしょうか。
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
独学で大学数学の複素数平面上の図形を勉強しています!
- 複素数平面 上の2つの円の交点を求め方
- 複素数平面 上における中心(1, 0)半径1の円周上の点(1/5, (3i/5)における円の接線の方程式
- 複素数平面上における中心(1/4, i/4)半径1/(2√2)の円周上の点(1/5, (3i/5)における円の接線の方程式