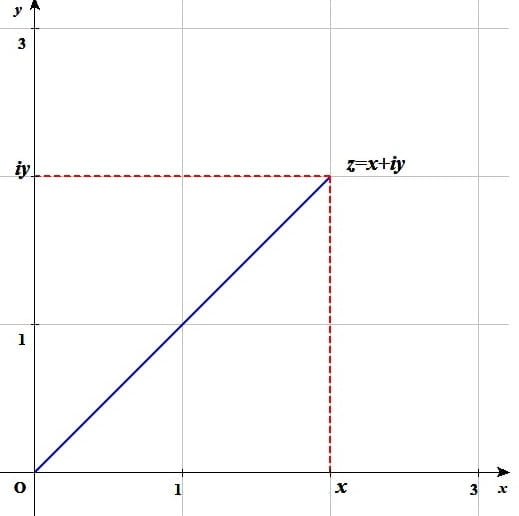
複素数平面上 における中心\(\left(\frac{1}{4},\ \frac{1}{4}i\right)\)半径\(\frac{1}{2\sqrt{2}}\)の円周上の点\(\left(\frac{1}{5},\ \frac{3}{5}i\right)\) における円の 接線の方程式
複素数平面上 における円の 接線の方程式 を求めるの必要な道具
※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。
目次
- 複素数平面上 における円の 接線の方程式 を求めるの必要な道具
- 複素数平面上 における円の 接線の方程式
- 複素数平面の直線の方程式の一般形
- 複素数平面上 における中心\(\left(\frac{1}{4},\ \frac{1}{4}i\right)\)半径\(\frac{1}{2\sqrt{2}}\)の円周上の点\(\left(\frac{1}{5},\ \frac{3}{5}i\right)\)における円の 接線の方程式
- 参考文献
- 座標平面での円の接線の方程式
- 座標平面での円の接線の方程式を求めるのに必要な道具
- 座標平面で中心(a, b)、半径rの円周上の点\((x_1,\ x_2)\)における接線の方程式
- 中心\(\left(\frac{1}{4}, \frac{1}{4}\right)\)、半径\(\frac{1}{2\sqrt{2}}\)の円周上の点\(\left(\frac{1}{5}, \frac{3}{5}\right)\)における接線の方程式
- 独学で大学数学の複素数平面上の図形を勉強しています!
複素数平面上 における円の 接線の方程式 を求めるの必要な道具
複素数平面上 における円の 接線の方程式
複素数平面上 における中心α半径rの円周上の点βにおける円の 接線の方程式
$$(\overline{\alpha}-\overline{\beta})z+(\alpha-\beta)\overline{z}-\alpha\overline{\alpha}+\beta\overline{\beta}+r^2=0$$
複素数平面の直線の方程式の一般形
$$\overline{\lambda}z-\lambda\overline{z}+\mu=0\ ただし、\muは純虚数$$
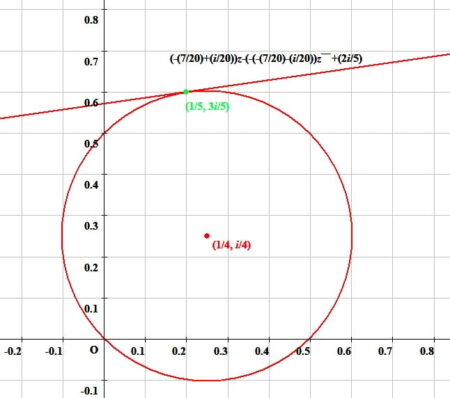
複素数平面上 における中心\(\left(\frac{1}{4},\ \frac{1}{4}i\right)\)半径\(\frac{1}{2\sqrt{2}}\)の円周上の点\(\left(\frac{1}{5},\ \frac{3}{5}i\right)\)における円の 接線の方程式
\((\overline{\alpha}-\overline{\beta})z+(\alpha-\beta)\overline{z}-\alpha\overline{\alpha}+\beta\overline{\beta}+r^2=0\)
$$\left(\left(\frac{1}{4}-\frac{1}{4}i\right)-\left(\frac{1}{5}-\frac{3}{5}i\right)\right)z+\left(\left(\frac{1}{4}+\frac{1}{4}i\right)-\left(\frac{1}{5}+\frac{3}{5}i\right)\right)\overline{z}-\frac{1}{8}+\frac{2}{5}+\frac{1}{8}=0$$
$$\left(\frac{5}{20}-\frac{4}{20}-\frac{5}{20}i+\frac{12}{20}i\right)z+\left(\frac{5}{20}-\frac{4}{20}+\frac{5}{20}i-\frac{12}{20}i\right)\overline{z}+\frac{2}{5}=0$$
$$\left(\frac{1}{20}+\frac{7}{20}i\right)z+\left(\frac{1}{20}-\frac{7}{20}i\right)\overline{z}+\frac{2}{5}=0\cdots①$$
複素数平面の直線の方程式の一般形
$$\left(-\frac{7}{20}+\frac{1}{20}i\right)z+\left(\frac{7}{20}+\frac{1}{20}i\right)\overline{z}+\frac{2}{5}i=0,\ \left(-\frac{7}{20}+\frac{1}{20}i\right)z-\left(-\frac{7}{20}-\frac{1}{20}i\right)\overline{z}+\frac{2}{5}i=0$$
参考文献
座標平面での円の接線の方程式
複素数平面の直線の方程式
$$\left(\frac{1}{20}+\frac{7}{20}i\right)z+\left(\frac{1}{20}-\frac{7}{20}i\right)\overline{z}+\frac{2}{5}=0\cdots①$$
①にz=x+yiを代入すると
$$\left(\frac{1}{20}+\frac{7}{20}i\right)(x+yi)+\left(\frac{1}{20}-\frac{7}{20}i\right)(x-yi)+\frac{2}{5}=0$$
$$\frac{1}{20}x-\frac{7}{20}y+\frac{1}{20}yi+\frac{7}{20}xi+\frac{1}{20}x-\frac{7}{20}y-\frac{1}{20}yi-\frac{7}{20}xi+\frac{2}{5}=0$$
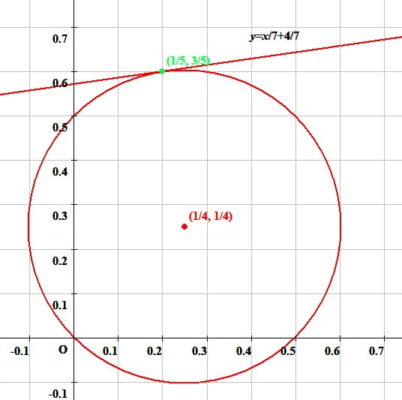
$$\frac{2}{20}x-\frac{14}{20}y+\frac{2}{5}=0,\ 2x-14y+8=0,\ x-7y+4=0,\ 7y=x+4,\ y=\frac{1}{7}x+\frac{4}{7}$$
座標平面での円の接線の方程式を求めるのに必要な道具
座標平面で中心(a, b)半径rの円周上の点\((x_1,\ y_1)\)における接線の方程式
座標平面で中心(a, b)、半径rの円周上の点\((x_1,\ x_2)\)における接線の方程式
$$(x_1-a)(x-a)+(y_1-b)(y-b)=r^2$$
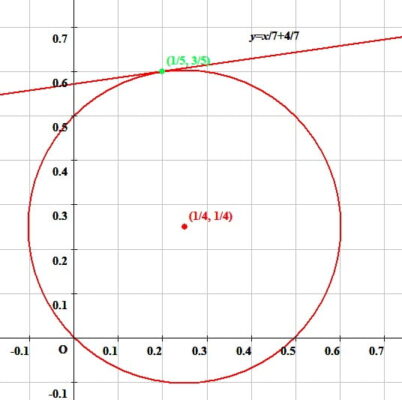
中心\(\left(\frac{1}{4}, \frac{1}{4}\right)\)、半径\(\frac{1}{2\sqrt{2}}\)の円周上の点\(\left(\frac{1}{5}, \frac{3}{5}\right)\)における接線の方程式
\((x_1-a)(x-a)+(y_1-b)(y-b)=r^2\)
$$\left(\frac{1}{5}-\frac{1}{4}\right)\left(x-\frac{1}{4}\right)+\left(\frac{3}{5}-\frac{1}{4}\right)\left(y-\frac{1}{4}\right)=\frac{1}{8}$$
$$\left(\frac{4}{20}-\frac{5}{20}\right)\left(x-\frac{1}{4}\right)+\left(\frac{12}{20}-\frac{5}{20}\right)\left(y-\frac{1}{4}\right)=\frac{1}{8}$$
$$-\frac{1}{20}x+\frac{1}{80}+\frac{7}{20}y-\frac{7}{80}=\frac{1}{8},\ -\frac{1}{20}x+\frac{7}{20}y-\frac{6}{80}-\frac{10}{80}=0,\ -\frac{1}{20}x+\frac{7}{20}y-\frac{16}{80}=0$$
$$-\frac{1}{20}x+\frac{7}{20}y-\frac{1}{5}=0,\ -x+7y-4=0,\ 7y=x+4,\ y=\frac{1}{7}x+\frac{4}{7}$$
検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
![]() を利用してみてはいかがでしょうか。
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
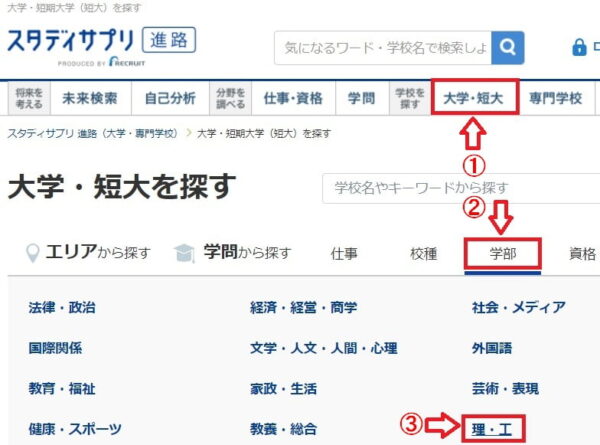
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
独学で大学数学の複素数平面上の図形を勉強しています!
- 複素数平面 上の2つの円の交点を求め方
- 複素数平面 上における中心(1, 0)半径1の円周上の点(1/5, (3i/5)における円の接線の方程式
- 複素数平面上における中心(1/4, i/4)半径1/(2√2)の円周上の点(1/5, (3i/5)における円の接線の方程式