∫(1/sin)=(1/2)log((1-cosx)/(1+cosx)), ∫(1/sin)=log tan(x/2)なので (1/2)log((1-cosx)/(1+cosx))からlog tan(x/2) を直接導いてみました。
\(\int\frac{1}{sin\ x}=\frac{1}{2}log\left(\frac{1-cos\ x}{1+cas\ x}\right),\ \int\frac{1}{sin\ x}=log\left(tan\frac{x}{2}\right)\)なので \(\frac{1}{2}log\left(\frac{1-cos\ x}{1+cas\ x}\right)からlog\left(tan\frac{x}{2}\right)\) を直接導いてみました。
※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。
目次
- \(\frac{1}{2}log\left(\frac{1-cos\ x}{1+cas\ x}\right)\)から\(log\left(tan\frac{x}{2}\right)\)を導くのに必要な道具 (1/2)log((1-cosx)/(1+cosx)) から log tan(x/2) を導くのに必要な道具
- sinの半角の公式
- cosの半角の公式
- \(\frac{1}{2}log\left(\frac{1-cos\ x}{1+cas\ x}\right)\)から\(log\left(tan\frac{x}{2}\right)\)を導く (1/2)log((1-cosx)/(1+cosx)) から log tan(x/2) を導く
- 大学数学入門(高校数学の復習)
\(\frac{1}{2}log\left(\frac{1-cos\ x}{1+cas\ x}\right)\)から\(log\left(tan\frac{x}{2}\right)\)を導くのに必要な道具 (1/2)log((1-cosx)/(1+cosx)) から log tan(x/2) を導くのに必要な道具
sinの半角の公式
$$sin^2\frac{\theta}{2}=\frac{1-cos\theta}{2}$$
sinの半角の公式の証明
cosの加法定理cos(α+β)=cosαcosβ-sinαsinβにおいてα=β=θとおくと
$$cos2\theta=cos^2\theta-sin^2\theta=1-2sin^2\theta$$
$$cos2\theta=1-2sin^2\theta,\ 2sin^2\theta=1-cos2\theta,\ sin^2\theta=\frac{1-cos2\theta}{2}$$
θを\(\frac{\theta}{2}\)に置き換えれば
$$sin^2\frac{\theta}{2}=\frac{1-cos\theta}{2}$$
cosの半角の公式
$$cos^2\frac{\theta}{2}=\frac{1+cos\theta}{2}$$
cosの半角の公式の証明
cosの加法定理cos(α+β)=cosαcosβ-sinαsinβにおいてα=β=θとおくと
$$cos2\theta=cos^2\theta-sin^2\theta=2cos^2\theta-1$$
$$cos2\theta=2cos^2\theta-1,\ 2cos^2\theta=1+cos2\theta,\ cos^2\theta=\frac{1+cos2\theta}{2}$$
θを\(\frac{\theta}{2}\)に置き換えれば
$$cos^2\frac{\theta}{2}=\frac{1+cos\theta}{2}$$
\(\frac{1}{2}log\left(\frac{1-cos\ x}{1+cas\ x}\right)\)から\(log\left(tan\frac{x}{2}\right)\)を導く (1/2)log((1-cosx)/(1+cosx)) から log tan(x/2) を導く
$$\frac{1}{2}log\left(\frac{1-cos\ x}{1+cas\ x}\right)=log\left(\frac{1-cos\ x}{1+cas\ x}\right)^{\frac{1}{2}}=log\left(\frac{\frac{1-cos\ x}{2}}{\frac{1+cas\ x}{2}}\right)^{\frac{1}{2}}=\left(\frac{sin^2\frac{x}{2}}{cos^2\frac{x}{2}}\right)^{\frac{1}{2}}=log\ tan\frac{x}{2}$$
検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
![]() を利用してみてはいかがでしょうか。
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
大学数学入門(高校数学の復習)
- (1-tan^2(x/2))/(1+tan^2(x/2))の解き方 倍角の公式
- (1/2)log((1-cosx)/(1+cosx))からlog tan(x/2)を導く
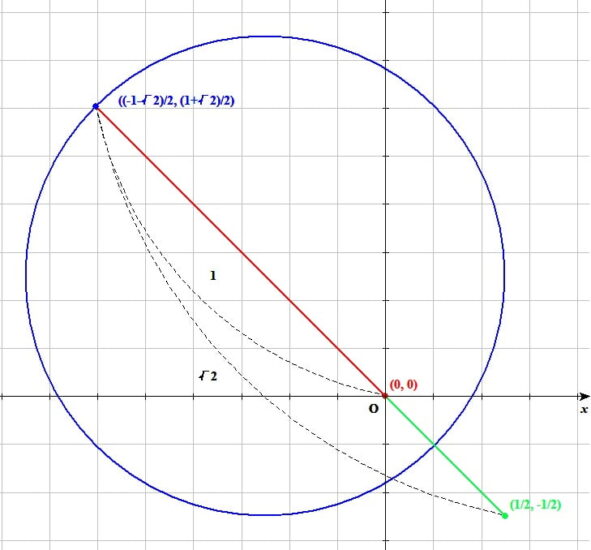
- 円(x-(2/7))^2+(y+(2/7))^2=(1/7)^2と直線y=-xの交点の座標
- 根号を含む線分の比