根号を含む線分の比を求めるに必要な道具
※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。
目次
- 二重根号の外し方
- 2点間の距離
- 根号を含む線分 の 比
- 根号を含む線分 ((4-√2)/14, (-4+√2)/14)と線分(1/4-(4-√2)/14, -1/4-(-4+√2)/14)の 比
- 根号を含む線分 ((4+√2)/14, (-4-√2)/14)と線分((4+√2)/14-1/4, (-4-√2)/14+1/4)の 比
- 根号を含む線分((-1+√2)/2, (1-√2)/2)と線分(1/2-(-1+√2)/2, -1/2-(1-√2)/2)の比
- 根号を含む線分((1+√2)/2, (-1-√2)/2)と線分(1/2-(-1-√2)/2, -1/2-(1+√2)/2)の比
- 独学で大学数学入門(高校数学の復習)
二重根号の外し方
$$\sqrt{(p+q)+2\sqrt{pq}}=\sqrt{p}+\sqrt{q}$$
足してp+q、掛けてpqの組み合わせを見つける。
根号内にマイナス記号がある場合は,p, qのうちの大きい方を前にして引き算をしないと\(\sqrt{p}-\sqrt{q}\)が正の数にならないことに注意。
2点間の距離
$$\overline{PQ}=\sqrt{(a_2-a_1)^2+(b_2-b_1)^2}$$
根号を含む線分 の 比
- 線分((4-√2)/14, (-4+√2)/14と線分(1/4-(4-√2)/14, -1/4-(-4+√2)/14)の比
- 線分((4+√2)/14, (-4-√2)/14)と線分((4+√2)/14-1/4, (-4-√2)/14+1/4)の比
- 線分((-1+√2)/2, (1-√2)/2)と線分(1/2-(-1+√2)/2, -1/2-(1-√2)/2)の比
- 線分((1+√2)/2, (-1-√2)/2)と線分(1/2-(-1-√2)/2, -1/2-(1+√2)/2)の比
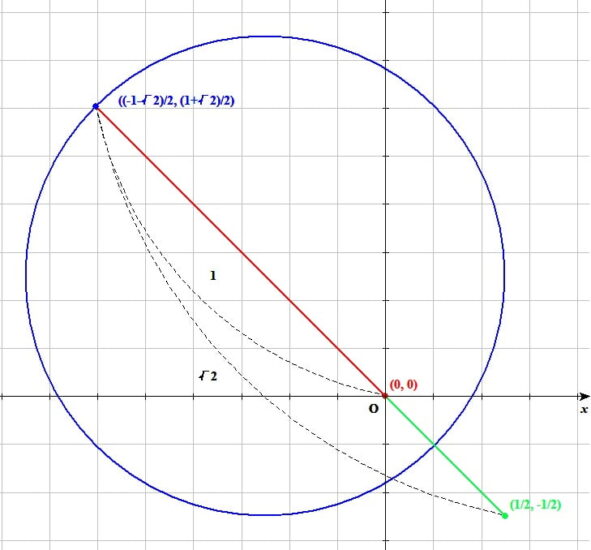
根号を含む線分 ((4-√2)/14, (-4+√2)/14)と線分(1/4-(4-√2)/14, -1/4-(-4+√2)/14)の 比
根号を含む線分 ((4-√2)/14, (-4+√2)/14) と線分 (1/4-(4-√2)/14, -1/4-(-4+√2)/14) の比 を求めるの必要な道具
- 二重根号の外し方
- 2点間の距離
線分\(\left(\frac{4-\sqrt{2}}{14},\ \frac{-4+\sqrt{2}}{14}\right)\)と線分\(\left(\frac{1}{4}-\frac{4-\sqrt{2}}{14},\ -\frac{1}{4}-\frac{-4+\sqrt{2}}{14}\right)\)の比

根号を含む線分 ((4+√2)/14, (-4-√2)/14)と線分((4+√2)/14-1/4, (-4-√2)/14+1/4)の 比
根号を含む線分((4+√2)/14, (-4-√2)/14)と線分((4+√2)/14-1/4, (-4-√2)/14+1/4)の比 を求めるの必要な道具
- 二重根号の外し方
- 2点間の距離
線分\(\left(\frac{4+\sqrt{2}}{14},\ \frac{-4-\sqrt{2}}{14}\right)\)と線分\(\left(\frac{4+\sqrt{2}}{14}-\frac{1}{4},\ \frac{-4-\sqrt{2}}{14}+\frac{1}{4}\right)\)の比
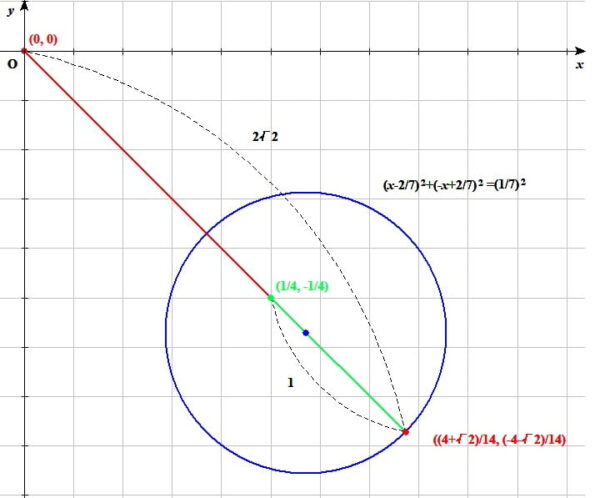
根号を含む線分((-1+√2)/2, (1-√2)/2)と線分(1/2-(-1+√2)/2, -1/2-(1-√2)/2)の比
根号を含む線分((-1+√2)/2, (1-√2)/2)と線分(1/2-(-1+√2)/2, -1/2-(1-√2)/2)の比 を求めるの必要な道具
- 二重根号の外し方
- 2点間の距離
線分\(\left(\frac{-1+\sqrt{2}}{2},\ \frac{1-\sqrt{2}}{2}\right)\)と線分\(\left(\frac{1}{2}-\frac{-1+\sqrt{2}}{2},\ -\frac{1}{2}-\frac{1-\sqrt{2}}{2}\right)\)の比
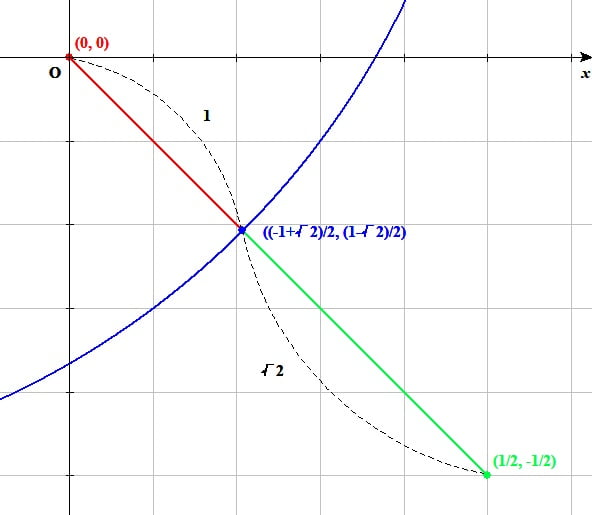
根号を含む線分((1+√2)/2, (-1-√2)/2)と線分(1/2-(-1-√2)/2, -1/2-(1+√2)/2)の比
根号を含む線分((1+√2)/2, (-1-√2)/2)と線分(1/2-(-1-√2)/2, -1/2-(1+√2)/2)の比 を求めるのに必要な道具
- 二重根号の外し方
- 2点間の距離
線分\(\left(\frac{1+\sqrt{2}}{2},\ \frac{-1-\sqrt{2}}{2}\right)\)と線分\(\left(\frac{1}{2}-\frac{-1-\sqrt{2}}{2},\ -\frac{1}{2}-\frac{1+\sqrt{2}}{2}\right)\)の比
検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
![]() を利用してみてはいかがでしょうか。
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
独学で大学数学入門(高校数学の復習)
- (1-tan^2(x/2))/(1+tan^2(x/2))の解き方 倍角の公式
- (1/2)log((1-cosx)/(1+cosx))からlog tan(x/2)を導く
- 円(x-(2/7))^2+(y+(2/7))^2=(1/7)^2と直線y=-xの交点の座標
- 根号を含む線分の比
