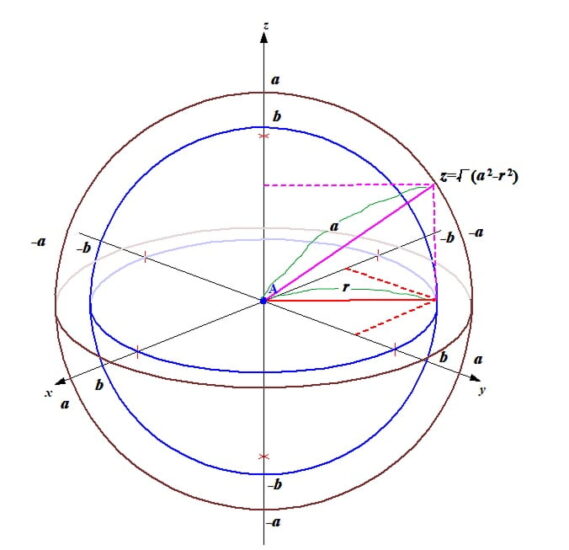
∫∫∫Vdxdydz V:|x|+|y|+|z|<=1 を解くのに必要な道具:絶対値記号のはずし方
\(\iiint_Vdxdydz\ V:|x|+|y|+|z|<=1\) の解き方が検索しても出てこなかったので記事にしました。
※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。
目次
\(\iiint_Vdxdydz\ V:|x|+|y|+|z|<=1\)を解くのに必要な道具 ∫∫∫Vdxdydz V:|x|+|y|+|z|<=1 を解くのに必要な道具
絶対値記号のはずし方
絶対値記号のはずし方
(1) 中身が正のとき
そのまま外す。 |x| = x
(2) 中身が負のとき
中身に「−(マイナス)」をつけて外す。 |x| = −x
\(\iiint_Vdxdydz\ V:|x|+|y|+|z|<=1\)の解法 ∫∫∫Vdxdydz V:|x|+|y|+|z|<=1 の解法
\(\iiint_Vdxdydz\ V:x+y+z<=1\)の解法 ∫∫∫Vdxdydz V:x+y+z<=1の解法
|x|,|y|,|z|の中身が全て正の場合
Vを満たす任意の座標(x,y,z)についてVの取り得る範囲は\(0\le z\le 1-x-y\)
zの積分範囲は[0→1-x-y]
上端の境界は x+y+z=1→ z=1-x-y
下端の境界は z=0
yの積分範囲は[0→1-x]
z=0のxy平面で
上端の境界は 0=1-x-y → y=1-x
下端の境界は y=0
xの積分範囲は[0→1]
上端の境界は 0=1-x → x=1
下端の境界は x=0
$$\iiint_Vdxdydz\ V:x+y+z<=1$$
$$=\int_{0}^{1}dx\int_{0}^{1-x}dy\int_{0}^{1-x-y}(x+y+z)dz$$
$$=\int_{0}^{1}dx\int_{0}^{1-x}dy\left[(x+y)z+\frac{z^2}{2}\right]^{z=1-x-y}_{z=0}$$
$$=\int_{0}^{1}dx\int_{0}^{1-x}\left((x+y)(1-x-y)+\frac{(1-x-y)^2}{2}\right)dy$$
$$=\int_{0}^{1}dx\int_{0}^{1-x}\left(\frac{(1-x-y)(2x+2y+1-x-y)}{2}\right)dy$$
$$=\int_{0}^{1}dx\int_{0}^{1-x}\left(\frac{(1-x-y)(x+y+1)}{2}\right)dy$$
$$=\int_{0}^{1}dx\int_{0}^{1-x}\frac{x+y+1-x^2-xy-x-xy-y^2-y}{2}dy$$
$$=\int_{0}^{1}dx\int_{0}^{1-x}\frac{1-x^2-2xy-y^2}{2}dy$$
$$=\frac{1}{2}\int_{0}^{1}dx\int_{0}^{1-x}( 1-x^2-2xy-y^2 )dy$$
$$= \frac{1}{2} \int_{0}^{1}dx\left[(1-x^2)y-xy^2-\frac{y^3}{3}\right]^{y=1-x}_{y=0}$$
$$= \frac{1}{2} \int_{0}^{1}\left((1-x)(1+x)(1-x)-x(1-x)^2-\frac{(1-x)^3}{3}\right)dx$$
$$= \frac{1}{2} \int_{0}^{1} \frac{(1-x)^2}{3}(3(1+x)-3x-(1-x))dx$$
$$= \frac{1}{6} \int_{0}^{1} (1-x)^2(2+x)dx$$
置換積分
1-x=tとおくと、x=1-t, \(\frac{dx}{dt}=-1,\) dx=-dt
x=0のときt=1、x=1のときt=0なので
$$\frac{1}{6} \int_{0}^{1} (1-x)^2(2+x)dx= \frac{1}{6} \int_{1}^{0} t^2(3-t)(-dt)= \frac{1}{6} \int_{0}^{1} (3t^2-t^3)dt= \frac{1}{6} \left[t^3-\frac{t^4}{4}\right]^{1}_{0}= \frac{1}{6 }\times\frac{3}{4}=\frac{1}{8}$$

絶対値を外すときの組み合わせは8通り
|x|の外し方(2通り)× |y|の外し方(2通り) × |z|の外し方(2通り) =8通り
xz平面およびyzに関してに対称な積分領域
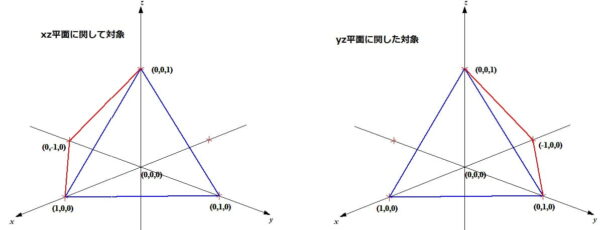
\(\iiint_Vdxdydz\ V:|x|+|y|+|z|<=1\)の解法 ∫∫∫Vdxdydz V:|x|+|y|+|z|<=1 の解法
x,y,zについての対称性から
$$\iiint_Vdxdydz\ V:|x|+|y|+|z|<=1$$
$$=8\iiint_Vdxdydz\ V:x+y+z<=1$$
$$=8 \times \frac{1}{8}=1$$

参考文献
検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
![]() を利用してみてはいかがでしょうか。
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
独学で大学数学の重積分を勉強をしています!
- ∫∫∫Vdxdydz V:|x|+|y|+|z|<=1の解き方
- ∫∫∫v sin(x+y+z)dxdydz V:0<=y<=x<=π/2,0<=z<=x+y
- ∫∫∫Vdxdydz V:x^2+y^2+z^2<=a^2, x^2+y^2<=b^2, (a>b>0)の解き方