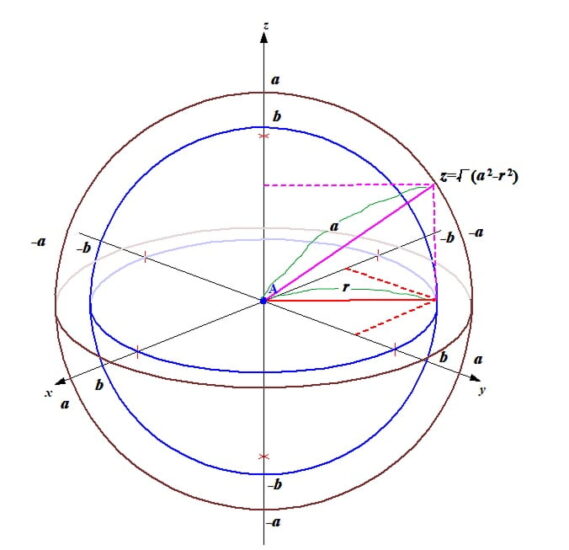
∫∫∫Vdxdydz V:x^2+y^2+z^2<=a^2 , x^2+y^2<=b^2 , (a>b>0) を解くのに必要な道具:二変数関数の極座標変換
\(\iiint_V dxdydz\ V:x^2+y^2+z^2\le a^2,\ x^2+y^2\le b^2\ (a>b>0)\)の解き方
※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。
目次
- \(\iiint_V dxdydz\ V:x^2+y^2+z^2\le a^2,\ x^2+y^2\le b^2\ (a>b>0)\)を解くのに必要な道具 ∫∫∫Vdxdydz V:x^2+y^2+z^2<=a^2, x^2+y^2<=b^2, (a>b>0) を解くのに必要な道具
- 二変数関数の極座標変換
- \(\iiint_V dxdydz\ V:x^2+y^2+z^2\le a^2,\ x^2+y^2\le b^2\ (a>b>0)\)の解法 ∫∫∫Vdxdydz V:x^2+y^2+z^2<=a^2, x^2+y^2<=b^2, (a>b>0) の解法
- \(\iiint_V dxdydz\ V:x^2+y^2+z^2\le a^2,\ x^2+y^2\le b^2\ (a>b>0)\)の解法 ∫∫∫Vdxdydz V:x^2+y^2+z^2<=a^2, x^2+y^2<=b^2, (a>b>0) の解法
- 参考文献
- 独学で大学数学の重積分を勉強をしています!
\(\iiint_V dxdydz\ V:x^2+y^2+z^2\le a^2,\ x^2+y^2\le b^2\ (a>b>0)\)を解くのに必要な道具 ∫∫∫Vdxdydz V:x^2+y^2+z^2<=a^2, x^2+y^2<=b^2, (a>b>0) を解くのに必要な道具
二変数関数の極座標変換
二変数関数の極座標変換
α,βは0≦β-α≦πを満たし、[α,β]で定義されたθの連続関数φ1(θ)とφ2(θ)が、この区間で \(0\le \varphi _{1} ( \theta ) \le \varphi _{2} ( \theta ) \) を満たすとする。このとき単純角領域
$$K=((rcos \theta ,rsin \theta )| \ \alpha \le\theta \le \beta , \ \varphi _{1} ( \theta ) \le r \le \varphi _{2} ( \theta ) )$$
で定義された連続関数f(x,y)に対して
$$\iint_K f(x,y)dxdy=\int_{ \alpha }^{ \beta }d \theta \int_{ \varphi _{1} ( \theta ) }^{ \varphi _{2} ( \theta ) }f(rcos \theta ,rsin \theta )rdr$$
となる。
\(\iiint_V dxdydz\ V:x^2+y^2+z^2\le a^2,\ x^2+y^2\le b^2\ (a>b>0)\)の解法 ∫∫∫Vdxdydz V:x^2+y^2+z^2<=a^2, x^2+y^2<=b^2, (a>b>0) の解法
積分範囲
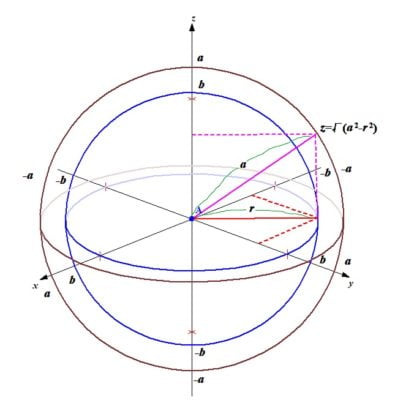
$$z=\pm\sqrt{a^2-x^2-y^2},\ -\sqrt{a^2-x^2-y^2}\le z\le \sqrt{a^2-x^2-y^2}$$
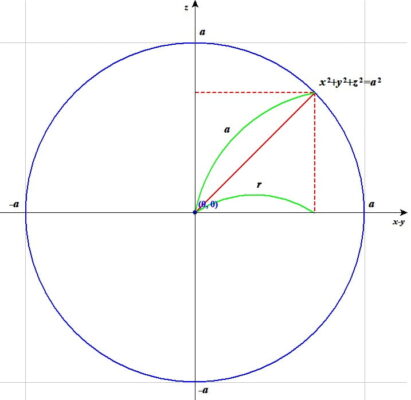
$$\int_{-\sqrt{a^2-r^2}}^\sqrt{a^2-r^2}dz=[z]_{-\sqrt{a^2-r^2}}^\sqrt{a^2-r^2}=2\sqrt{a^2-r^2}$$
\(D=\{(x,\ y)|x^2+y^2\le b^2\}\)とすると
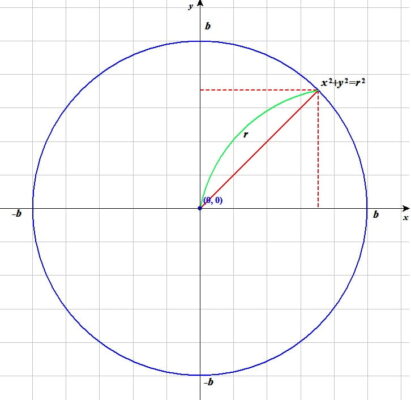
\(\iiint_V dxdydz\ V:x^2+y^2+z^2\le a^2,\ x^2+y^2\le b^2\ (a>b>0)\)の解法 ∫∫∫Vdxdydz V:x^2+y^2+z^2<=a^2, x^2+y^2<=b^2, (a>b>0) の解法
$$\iint_D 2\sqrt{a^2-x^2-y^2}dxdy=\int_0^{2\pi}d\theta \int_0^b 2\sqrt{a^2-r^2}rdr=4\pi\int_0^b (a^2-r^2)^{\frac{1}{2}}(a^2-r^2)’dr$$
$$=4\pi\left(-\frac{1}{2}\right)\left[\frac{2}{3}(a^2-r^2)^{\frac{3}{2}}\right]_0^b=-2\pi\left(\frac{2}{3}(a^2-b^2)^{\frac{3}{2}}-\frac{2}{3}a^3\right)=\frac{4}{3}\pi\left(a^3-(a^2-b^2)^{\frac{3}{2}}\right)$$
参考文献
検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
![]() を利用してみてはいかがでしょうか。
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
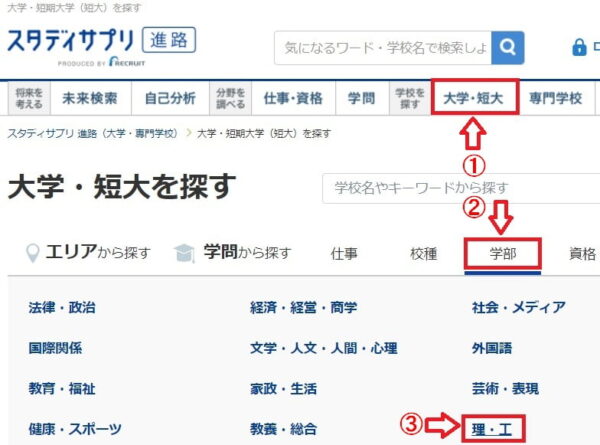
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
独学で大学数学の重積分を勉強をしています!
- ∫∫∫Vdxdydz V:|x|+|y|+|z|<=1の解き方
- ∫∫∫v sin(x+y+z)dxdydz V:0<=y<=x<=π/2,0<=z<=x+y
- ∫∫∫Vdxdydz V:x^2+y^2+z^2<=a^2, x^2+y^2<=b^2, (a>b>0)の解き方