∫∫∫v sin(x+y+z)dxdydz V:0<=y<=x<=π/2 ,0<=z<=x+y を解くのに必要な道具:固定された変数の値に依存する積分区間を先に積分する。
※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。
目次
- \(\iiint_V sin(x+y+z)dxdydz\ V:0\le y\le x\le\frac{\pi}{2},\ 0\le z\le x+y\)を解くのに必要な道具 ∫∫∫v sin(x+y+z)dxdydz V:0<=y<=x<=π/2 ,0<=z<=x+y を解くのに必要な道具
- 積分区間
- \(\iiint_V sin(x+y+z)dxdydz\ V:0\le y\le x\le\frac{\pi}{2},\ 0\le z\le x+y\)の解法 ∫∫∫v sin(x+y+z)dxdydz V:0<=y<=x<=π/2 ,0<=z<=x+y の解法
- 参考文献
- 独学で大学数学の重積分を勉強をしています!
\(\iiint_V sin(x+y+z)dxdydz\ V:0\le y\le x\le\frac{\pi}{2},\ 0\le z\le x+y\)を解くのに必要な道具 ∫∫∫v sin(x+y+z)dxdydz V:0<=y<=x<=π/2 ,0<=z<=x+y を解くのに必要な道具
固定された変数の値に依存する積分区間を先に積分 する。
積分区間
固定された変数の値に依存する積分区間を先に積分 する。
\(\iiint_V sin(x+y+z)dxdydz\ V:0\le y\le x\le\frac{\pi}{2},\ 0\le z\le x+y\)の解法 ∫∫∫v sin(x+y+z)dxdydz V:0<=y<=x<=π/2 ,0<=z<=x+y の解法
積分区間
$$0\le x\le \frac{\pi}{2},\ 0\le y\le x,\ 0\le z\le x+y$$
1変数関数の積分を3度行う累次積分
$$\iiint_V sin(x+y+z)dxdydz=\int_0^\frac{\pi}{2}dx\int_0^xdy\int_0^{x+y}sin(x+y+z)dz$$
$$=-\int_0^\frac{\pi}{2}dx\int_0^xdy[cos(x+y+z)]^{x+y}_0=-\int_0^\frac{\pi}{2}dx\int_0^x(cos(2x+2y)-cos(x+y))dy$$
$$=-\int_0^\frac{\pi}{2}dx\left[\frac{1}{2}sin(2x+2y)-sin(x+y)\right]^x_0=-\int_0^\frac{\pi}{2}\left(\left(\frac{1}{2}sin4x-sin2x\right)-\left(\frac{1}{2}sin2x-sinx\right)\right)dx$$
$$=-\frac{1}{2}\int_0^\frac{\pi}{2}\left(sin4x-3sin2x+2sinx\right)dx =\frac{1}{2}\left[\frac{1}{4}cos4x-\frac{3}{2}cos2x+2cosx\right]^{\frac{\pi}{2}}_0$$
$$=\frac{1}{8}(cos2\pi-6cos\pi+8cos\frac{\pi}{2}-(cos0-6cos0+8cos0))$$
$$=\frac{1}{8}(1+6-(1-6+8))=\frac{1}{8}(7-3)=\frac{4}{8}=\frac{1}{2}$$
参考文献
検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
![]() を利用してみてはいかがでしょうか。
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
独学で大学数学の重積分を勉強をしています!
- ∫∫∫Vdxdydz V:|x|+|y|+|z|<=1の解き方
- ∫∫∫v sin(x+y+z)dxdydz V:0<=y<=x<=π/2,0<=z<=x+y
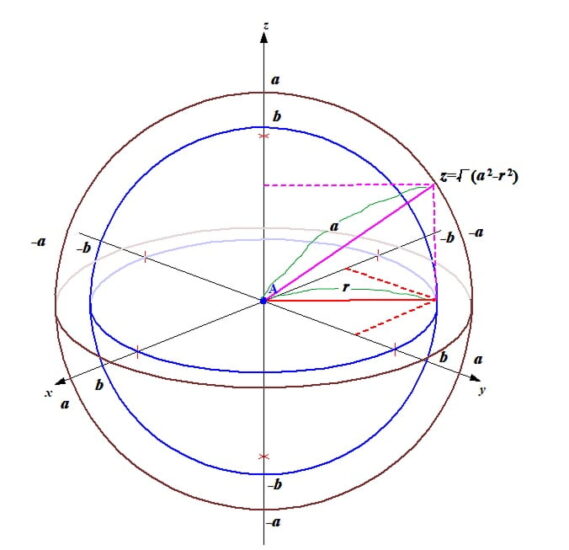
- ∫∫∫Vdxdydz V:x^2+y^2+z^2<=a^2, x^2+y^2<=b^2, (a>b>0)の解き方