∫1/√(x^2+1)dx を解くのに必要な道具 置換積分
※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。
目次
\(\int\frac{1}{\sqrt{x^2+1}}dx\)を解くのに必要な道具 ∫1/√(x^2+1)dx を解くのに必要な道具
置換積分
置換積分
関数f(x)が連続であり、関数φ(t)は、微分可能で導関数がφ'(t)が連続とする。このとき
$$\int f(x)dx=\int f(\varphi(t))\varphi'(t)dt$$
が成り立つ。
\(\int\frac{1}{\sqrt{x^2+1}}dx\)の解法 ∫1/√(x^2+1)dx の解法
x=tanθとおくと
\(\frac{dx}{d\theta}=\frac{1}{cos^2\theta},\ dx=\frac{1}{cos^2\theta}d\theta\)
\(\int\frac{1}{\sqrt{x^2+1}}dx\)
$$=\int\frac{1}{\sqrt{1+tan^2\theta}}\frac{1}{cos^2\theta}d\theta=\int\frac{1}{\sqrt{\frac{1}{cos^2\theta}}}\frac{1}{cos^2\theta}d\theta=\int\frac{1}{\frac{1}{cos\theta}}\frac{1}{cos^2\theta}d\theta=\int cos\theta\frac{1}{cos^2\theta}d\theta=\int\frac{cos\theta}{1-sin^2\theta}d\theta$$
t=sinθとおくと
\(\frac{dt}{d\theta}=cos\theta,\ dt=cos\theta d\theta\)
\(\int\frac{1}{\sqrt{x^2+1}}dx\)
$$=\int\frac{cos\theta}{1-sin^2\theta}d\theta=\int\frac{1}{1-t^2}dt=\frac{1}{2}\int\frac{1}{1+t}dt+\frac{1}{2}\int\frac{1}{1-t}dt =\frac{1}{2}\int\frac{1}{t+1}dt-\frac{1}{2}\int\frac{1}{t-1}dt$$
$$=\frac{1}{2}log|t+1|-\frac{1}{2}log|t-1|+A=\frac{1}{2}log\left|\frac{t+1}{t-1}\right|+A=\frac{1}{2}log\left|\frac{1+t}{1-t}\right|+A$$
$$=\frac{1}{2}log\left|\frac{1+sin\theta}{1-sin\theta}\right|+A=\frac{1}{2}log\left|\frac{(1+sin\theta)^2}{1-sin^2\theta}\right|+A=\frac{1}{2}log\left|\frac{(1+sin\theta)^2}{cos^2\theta}\right|+A$$
$$=\frac{1}{2}log\left(\frac{1+sin\theta}{cos\theta}\right)^2+A=log\left(\frac{1+sin\theta}{cos\theta}\right)+A=log\left(\frac{sin\theta}{cos\theta}+\frac{1}{cos\theta}\right)+A$$
$$=log\left(tan\theta+\sqrt{\frac{1}{cos^2\theta}}\right)+A=log\left(tan\theta+\sqrt{1+\tan^2\theta}\right)+A=log\left(x+\sqrt{1+x^2}\right)+A$$
参考文献
検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
![]() を利用してみてはいかがでしょうか。
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
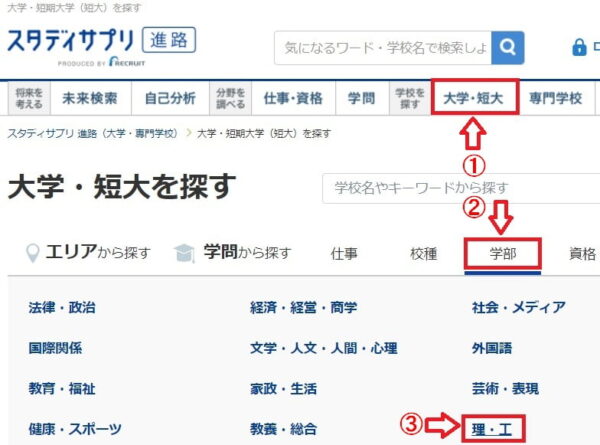
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
独学で大学数学の置換積分を勉強しています!
