∫(logloglogx)/x・logxdx を解くのに必要な道具
\(\int{\frac{logloglog(x)}{x・log(x)}}dx\)の解き方を検索しても出てこなかったので記事にしました。
※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。
目次
\(\int{\frac{logloglog(x)}{x・log(x)}}dx\) 解くのに必要な道具 ∫(logloglogx)/x・logxdx を解くのに必要な道具
置換積分
$$\int{f( \varphi (x)) \varphi ’(x)}dx=\int_{}{}{f(t)}dx$$
φ(x)=tとする。
対数関数の不定積分
$$\int{log(x)}dx=x・logx-x$$
証明
部分積分\(\int{f(x)g(x)}dx=F(x)g(x)-\int{F(x)g^{\prime} (x)}dx\)を使って
$$\int{1・log(x)}dx=x・log(x)-\int{x・\frac{1}{x}}dx=x・log(x)-x$$
\(\int{\frac{logloglogx}{xlogx}}dx\)の解法 ∫(logloglogx)/x・logxdx の解法
loglog(x)=tとおく
$$t= \varphi (x)=loglog(x)$$
$$\varphi ^{\prime} (x) =\frac{1}{x・log(x)}$$
$$\int{\frac{logloglog(x)}{x・log(x)}}dx=\int{log(loglog(x) ) ^{\prime} logloglog(x)}dx=\int{log(t)}dt$$
$$=t・log(t)-t=loglog(x)・logloglog(x)-loglog(x)$$
たまたま、loglog(x)=tとおくことに気づけたので解けました。
参考文献
リンク
検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
ココナラ 登録方法 会員登録しなくてもサービスの検索はできます。サービスの購入・出品には会員登録が必要です。会員登録をクリック メールアドレスを入力して メール…
jikuu.site
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
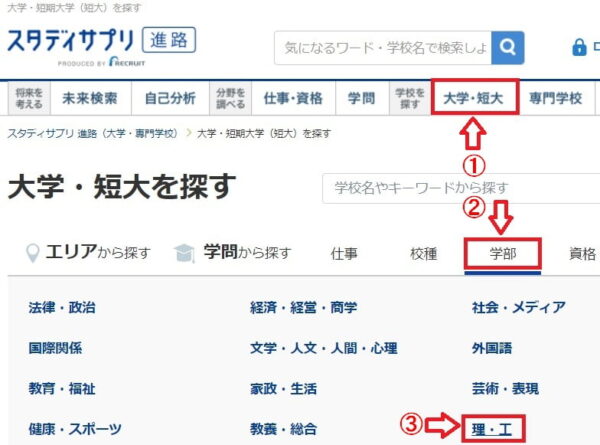
スタディサプリ進路 社会人向け の 使い方 スタディサプリ進路 社会人向け の 使い方 スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます…
jikuu.work
独学で大学数学の置換積分を勉強しています！
置換積分 とは適当な置き換えによって積分変数を変更 して、そのままでは積分が難しい関数を積分する方法です。 ∫(logloglogx)/x・logxdx の解き…
jikuu.work