∫[0→π]cosθ/(5-4cosθ)dθ の解き方

∫[0→π]cosθ/(5-4cosθ)dθ を解くのに必要な道具

三角関数の有理関数
留数の原理を用いた定積分の計算

$\int_{0}^{ \pi }\frac{cos\theta}{5-4cos\theta}d\theta$の解き方が検索しても出てこなかったので記事にしました。

※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。

$\int_{0}^{ \pi }\frac{cos\theta}{5-4cos\theta}d\theta$を解くのに必要な道具 ∫[0→π]cosθ/(5-4cosθ)dθ を解くのに必要な道具
三角関数の有理関数
留数の原理を用いた定積分の計算
$\int_{0}^{ \pi }\frac{cos\theta}{5-4cos\theta}d\theta$ の解法 ∫[0→π]cosθ/(5-4cosθ)dθ の解法
- 被積分関数の整理
- $-2(2z^2-5z+2)=0$の計算
$\int_{0}^{ \pi }\frac{cos\theta}{5-4cos\theta}d\theta$ の解法 ∫[0→π]cosθ/(5-4cosθ)dθ の解法
参考文献
独学で大学数学の留数を勉強しています！

$\int_{0}^{ \pi }\frac{cos\theta}{5-4cos\theta}d\theta$を解くのに必要な道具 ∫[0→π]cosθ/(5-4cosθ)dθ を解くのに必要な道具

三角関数の有理関数
留数の原理を用いた定積分の計算

三角関数の有理関数

$z=e^{2i\theta}$とおくと、θが0からπまで変化するとき、zは複素平面上で、原点を中心とする単位円C:|z|=1の周上を正の向きに1周する。

f(x,y)を有理関数としたとき

$$\int_{0}^{\pi}f(cos\theta,sin\theta)d\theta=\frac{1}{2i}\int_{|z|=1}f\left(\frac{1}{2}\left(z+\frac{1}{z} \right) ,\frac{1}{2i}\left(z-\frac{1}{z}\right)\right)\frac{dz}{z}$$

である。

留数の原理を用いた定積分の計算

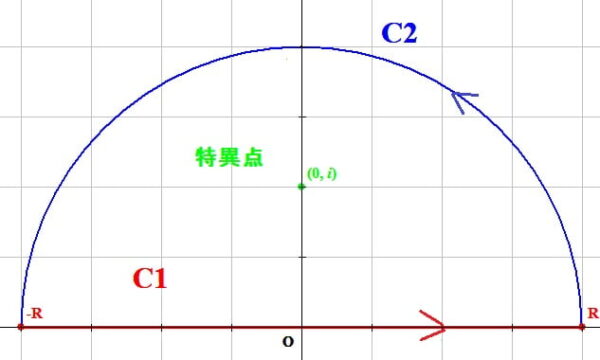
関数f(z)は上半平面Imz≧0で、実軸上にない有限個の極$ \alpha _1, \alpha_2,\cdots, \alpha_ n$を除いて正則で

$$\lim_{z \to \infty}z f(z)=0$$

とする。このとき

$$\int_{-\infty}^{\infty}f(x)dx=2\pi i\sum_{l=1}^{n}Res_{z=\alpha l} \ f(z)$$

である。

$\int_{0}^{ \pi }\frac{cos\theta}{5-4cos\theta}d\theta$ の解法 ∫[0→π]cosθ/(5-4cosθ)dθ の解法

被積分関数の計算が面倒なので前もって計算しておきます。

被積分関数の整理

$$\frac{cos\theta}{5-4cos\theta}=\frac{\frac{1}{2}\left(z+\frac{1}{z}\right)}{5-2\left(z+\frac{1}{z} \right) }=\frac{z+\frac{1}{z}}{10-4\left(z+\frac{1}{z} \right) }=\frac{z+\frac{1}{z}}{10-4z-\frac{4}{z}}=\frac{z^2+1}{-4z^2+10z-4}=\frac{z^3+z}{-2z(2z^2-5z+2)}$$

$-2(2z^2-5z+2)=0$の計算

$$-2z(2z^2-5z+2)=0$$

$$z(2z^2-5z+2)=0$$

$$z(2z-1)(z-2)=0$$

$$z=0,\ \frac{1}{2},\ 2$$

よって被積分関数は|z|<1に2個の1位の極z=0, $z=\frac{1}{2}$をもつ。

$\int_{0}^{ \pi }\frac{cos\theta}{5-4cos\theta}d\theta$ の解法 ∫[0→π]cosθ/(5-4cosθ)dθ の解法

$$\int_{0}^{ \pi }\frac{cos\theta}{5-4cos\theta}d\theta=\frac{1}{-4i}\int_{|z|=1}\frac{(z^2+1)z}{2z^3-5z^2+2z}\frac{dz}{z}=-\frac{\pi}{2}\left(Res_{z=0} f(z)+Res_{z=\frac{1}{2}}f(z)\right)$$

$$=-\frac{\pi}{2}\left( \left[\frac{z^2+1}{6z^2-10z+2}\right]_{z=0}+ \left[\frac{z^2+1}{6z^2-10z+2}\right]_{z=\frac{1}{2}} \right)= -\frac{\pi}{2}\left( \frac{1}{2}+\frac{\frac{1}{4}+\frac{4}{4}}{\frac{3}{2}-5+2 }\right)= -\frac{\pi}{2}\left( \frac{1}{2}+\frac{\frac{5}{4}}{\frac{3-10+4}{2} }\right)$$

$$= -\frac{\pi}{2}\left( \frac{1}{2}+\frac{\frac{5}{4}}{\frac{-3}{2} }\right)= -\frac{\pi}{2}\left( \frac{1}{2}-\frac{5}{6}\right)= -\frac{\pi}{2}\left( \frac{3}{6}-\frac{5}{6}\right)= -\frac{\pi}{2}\left(- \frac{2}{6}\right)=\frac{\pi}{6}$$