∫[0→∞](xsinx/(1+x^2))dx の解き方

∫[0→∞](xsinx/(1+x^2))dx を解くのに必要な道具

偶関数・奇関数の定積分の性質
複素数の絶対値の外し方
ジョルダンの不等式
その他

$\int_{0}^{ \infty }\frac{x\ sinx}{1+x^2}dx$の解き方を検索しても正しい解法が出てこなかったので記事にしました。

※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。

$\int_{0}^{ \infty }\frac{x\ sinx}{1+x^2}dx$を解くのに必要な道具 ∫[0→∞](xsinx/(1+x^2))dx を解くのに必要な道具
偶関数・奇関数の定積分の性質
- 偶関数・奇関数の積
複素数の絶対値の外し方
ジョルダンの不等式
その他
$\int_{0}^{ \infty }\frac{x\ sinx}{1+x^2}dx$ の解法 ∫[0→∞](xsinx/(1+x^2))dx の解法
- $C_1$：-R->R の計算
- $C_2$ ：原点中心の半径Rの上半径を反時計回りに積分
$\int_{0}^{ \infty }\frac{x\ sinx}{1+x^2}dx$ の解法 ∫[0→∞](xsinx/(1+x^2))dx の解法
参考文献
独学で大学数学の留数を勉強しています！

$\int_{0}^{ \infty }\frac{x\ sinx}{1+x^2}dx$を解くのに必要な道具 ∫[0→∞](xsinx/(1+x^2))dx を解くのに必要な道具

偶関数・奇関数の定積分の性質
複素数の絶対値の外し方
ジョルダンの不等式
その他

偶関数・奇関数の定積分の性質

f(x)が偶関数のとき

$$\int_{-a}^a f(x)dx=2\int_0^a f(x)dx$$

f(x)が奇関数のとき

$$\int_{-a}^a f(x)dx=0$$

偶関数・奇関数の積

奇関数×奇関数＝偶関数
奇関数×偶関数＝奇関数
偶関数×偶関数＝偶関数

複素数の絶対値の外し方

|i|

i=0+1・iなので

$$|i|=\sqrt {0^2+1^2}=1$$

$|e^z|$

$$|e^z|=|e^{x+iy}|=|e^x \cdot e^{iy}|=|e^x||e^{iy}|=e^x \cdot 1=e^x$$

$$|e^{iy}|=\sqrt{|e^{iy}|^2}=\sqrt{(e^{iy})\overline{(e^{iy})}}=\sqrt{(cosy+i\ siny)(cosy-i\ siny)}$$

$$=\sqrt{cos^2y+sin^2y}=1\cdots①$$

$|e^{iRcos\ \theta}|$

$$|e^{iRcos\theta}|=\sqrt{|e^{iRcos\theta}|^2}=\sqrt{(e^{iRcos\theta})\overline{(e^{iRcos\theta})}}=\sqrt{(e^{iRcos\theta})(e^{-iRcos\theta})}=\sqrt{e^0}=1\cdots②$$

ジョルダンの不等式

$$sin\theta\ge\frac{2\theta}{\pi}$$

その他

$$R^2-1=|R^2e^{2i\theta}+1-1|-1（①より）$$

$$\le|R^2e^{2i\theta}+1|+1-1=|1+R^2e^{2i\theta}|$$

$\int_{0}^{ \infty }\frac{x\ sinx}{1+x^2}dx$ の解法 ∫[0→∞](xsinx/(1+x^2))dx の解法

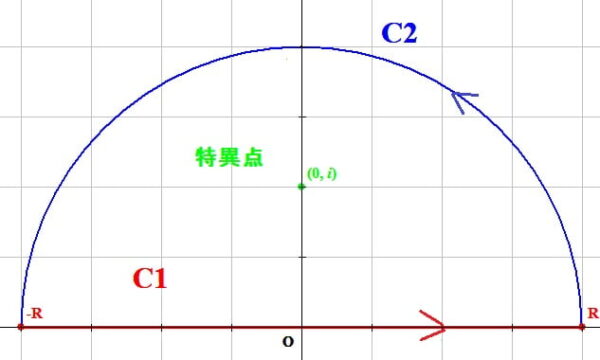
$C_1$：-R->R の計算

$f(z)=\frac{ze^{iz}}{1+z^2}$を$C_1$：-R->R、$C_2$：原点中心の半径Rの上半径を反時計回りに積分する。

$$\int_{C_1}f(z)dz=\int_{-R}^{R}\frac {x\ e^{ix}}{1+x^2}dx=\int_{-R}^{R}\frac {x\ cosx}{1+x^2}dx+i \int_{-R}^{R}\frac {x\ sinx}{1+x^2}dx = i \int_{-R}^{R}\frac {x\ sinx}{1+x^2}dx $$

$C_2$ ：原点中心の半径Rの上半径を反時計回りに積分

$f(z)=\frac{ze^{iz}}{1+z^2}$を$C_1$：-R->R、$C_2$：原点中心の半径Rの上半径を反時計回りに積分する。

$C_2$上の点を$z=Re^{i \theta }$とすると$dz=i Re^{i\theta}d\theta$

$$\int_{C_2}\left|\frac{ze^{iz}}{1+z^2}dz\right|=\int_{0}^{\pi}\left|\frac{Re^{i\theta}e^{iRe^{i\theta}}}{1+R^2e^{i2\theta}}iRe^{i\theta}d\theta\right|=\int_{0}^{\pi}\frac{R^2|e^{iRe^{i\theta}}|}{|1+R^2|}d\theta =\int_{0}^{\pi}\frac{R^2|e^{iRcos\theta-Rsin\theta}|}{|1+R^2|}d\theta$$

$$\le \frac{2R^2}{R^2-1}\int_{0}^{\frac{\pi}{2}}e^{-Rsin\theta}d\theta（②より）$$

$$\le \frac{2R^2}{R^2-1}\int_{0}^{\frac{\pi}{2}}e^{-R\frac{2\theta}{\pi}}d\theta=\frac{2R^2}{R^2-1} \left[-\frac{\pi}{2R}e^{\frac{-2R}{\pi}\theta}\right]^\frac{\pi}{2}_0=\frac{2R^2}{R^2-1} \left(-\frac{\pi}{2R}e^{-R}+ \frac{\pi}{2R}\right) $$

$$ \lim_{R \to \infty} \frac{2R^2}{R^2-1} \left(-\frac{\pi}{2R}e^{-R}+ \frac{\pi}{2R}\right)=0 $$

$\int_{0}^{ \infty }\frac{x\ sinx}{1+x^2}dx$ の解法 ∫[0→∞](xsinx/(1+x^2))dx の解法

$$\int_{0}^{ \infty }\frac{x\ sinx}{1+x^2}dx=\frac{1}{2}\int_{- \infty }^{ \infty }\frac{x\ sinx}{1+x^2}dx=\frac{1}{2i}\int_{- \infty }^{ \infty }\frac{xe^{ix}}{1+x^2}dx$$

$$=\frac{1}{2i} 2\pi i Res f(z)=\pi[(z-i)f(z)]_{z=i}=\pi\frac{ie^{-1}}{2i}=\frac{\pi}{2e}$$