積分因子の求め方
※数式がスマホで画面からはみ出る場合、横スクロールするかピンチインしてください。
目次
言葉の定義
全微分方程式
P(x,y)dx+Q(x,y)dy=0の形の方程式を全微分方程式という。
完全微分条件
P(x,y)dx+Q(x,y)dyがある関数の全微分になっている条件
$$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$$
積分因子
P(x,y)dx+Q(x,y)dy=0が完全微分条件をみたしていない場合
\(\frac{\partial \lambda P}{\partial y}=\frac{\partial \lambda Q}{\partial x}\)を満たすように\(\lambda(x,y)P(x,y)dx+\lambda(x,y) Q(x,y)dy=0\)と書きなおす。
この\(\lambda(x,y)\)を積分因子という。
積分因子の求め方
\((xy^2+xy^2cos\ x+xy\ cox\ y)dx+(xy\ sin\ x-x^2y\ sin\ y+x^2y)dy=0\)の積分因子
\(P=xy^2+xy^2cos\ x+xy\ cos\ y,\ Q=xy\ sin\ x-x^2y\ sin\ y+x^2yとすると\frac{\partial P}{\partial y}\neq\frac{\partial Q}{\partial x}\)であるから、完全微分方程式ではない。
完全微分条件
$$\frac{\partial \lambda P}{\partial y}=\frac{\partial \lambda Q}{\partial x},\ \frac{\partial}{\partial y}(\lambda(xy^2+xy^2cos\ x+xy\ cox\ y))=\frac{\partial}{\partial x}(\lambda(xy\ sin\ x-x^2y\ sin\ y+x^2y))$$
$$\frac{\partial\lambda }{\partial y}(xy^2+xy^2cos\ x+xy\ cox\ y)+\lambda(2xy+2xy\ cos\ x+x\ cos\ y-xy\ sin\ y)$$
$$=\frac{\partial\lambda}{\partial x}(xy\ sin\ x-x^2y\ sin\ y+x^2y)+\lambda(y\ sin\ x+xy\ cos\ x-2xy\ sin\ y+2xy)$$
$$(xy^2+xy^2cos\ x+xy\ cox\ y)\frac{\partial\lambda }{\partial y}-(xy\ sin\ x-x^2y\ sin\ y+x^2y)\frac{\partial\lambda}{\partial x}$$
$$=-\lambda(2xy+2xy\ cos\ x+x\ cos\ y-xy\ sin\ y-y\ sin\ x-xy\ cos\ x+2xy\ sin\ y-2xy)$$
$$=-\lambda(xy\ cos\ x+x\ cos\ y+xy\ sin\ y-y\ sin\ x)$$
\(\lambda=x^my^nとおくと\frac{\partial \lambda}{\partial y}=nx^my^{n-1},\ \frac{\partial \lambda}{\partial x}=mx^{n-1}y^n\)
$$左辺=(xy^2+xy^2cos\ x+xy\ cox\ y)nx^my^{n-1}-(xy\ sin\ x-x^2y\ sin\ y+x^2y)mx^{n-1}y^n$$
$$=nx^{m+1}y^{n+1}+nx^{m+1}y^{n+1}cos\ x+nx^{m+1}y^n\ cox\ y-mx^m y^{n+1}\ sin\ x+mx^{m+1}y^{n+1} sin\ y-mx^{m+1}y^{n+1}$$
$$=(n-m)x^{m+1}y^{n+1}+nx^{m+1}y^{n+1}cos\ x+nx^{m+1}y^n\ cox\ y-mx^m y^{n+1}\ sin\ x+mx^{m+1}y^{n+1} sin\ y$$
$$右辺=-x^my^n(xy\ cos\ x+x\ cos\ y+xy\ sin\ y-y\ sin\ x)$$
$$=-x^{m+1}y^{n+1}\ cos\ x-x^{m+1}y^n\ cos\ y-x^{m+1}y^{n+1}\ sin\ y+x^my^{n+1}\ sin\ x)$$
係数を比較し
$$n=-1,\ m=-1,\ 積分因子\lambda=\frac{1}{xy}$$
参考文献
検索しても計算過程が見つからない場合
検索しても計算過程が見つからない場合ココナラ
![]() を利用してみてはいかがでしょうか。
を利用してみてはいかがでしょうか。
ココナラ 登録方法
会員登録しなくてもサービスの検索はできます。
サービスの購入・出品には会員登録が必要です。
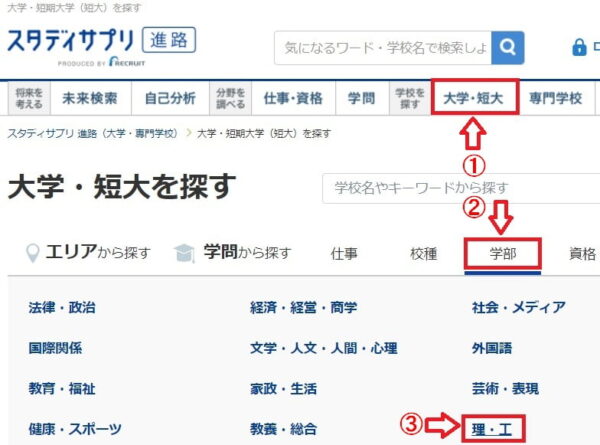
スタディサプリ進路 社会人向け の 使い方
スタディサプリ進路 社会人向けで社会人が数学を学べる大学を検索してみます。
独学で大学数学の 積分因子 を勉強しています!
- (2x^4y+2x^3y+11x^2y^2+2x^3y^2+9xy^3)dy+(3x^3y^2+2x^2y^2+5xy^3+3x^2y^3+3y^4)dx=0の解き方
- (x^2+3xy+2y^2)dy+(2x^2+3xy+y^2)dx=0の解き方
- 積分因子 の求め方
- (-xy sinx siny+x^2y)dy+(xy cosx cosy+xy^2)dx=0の 積分因子
